Conjunción, del latín
coniunctĭo, es una
junta o
unión.
En concreto, esta palabra latina se encuentra conformada por tres
partes claramente delimitadas: el prefijo “con-“, que es sinónimo de
“completamente”; el vocablo “iugum”, que es equivalente a “yugo”, y por
último el sufijo “-ción”, que puede traducirse como “acción y efecto”.
El término se utiliza en la
astronomía y en la
lingüística, entre otros ámbitos. Por ejemplo:
“Los astrónomos informaron que mañana se producirá la conjunción entre Mercurio y Venus”,
“Tengo que explicar lo que es una conjunción coordinante”,
“La maestra dijo que el próximo cuatrimestre estudiaremos las conjunciones”.
Una
conjunción astronómica es la situación relativa
de dos o más astros cuando, desde un punto de observación, se encuentran
alineados. El concepto también se utiliza para nombrar al aspecto de
dos astros que ocupan la misma casa celeste.
Es posible hablar de
conjunción inferior o
conjunción superior. La conjunción inferior tiene lugar cuando los planetas interiores a la órbita terrestre pasan entre la
Tierra y el
Sol, lo que hace que dichos
planetas se encuentren cerca de la
Tierra y exhiban su cara no iluminada.
La conjunción superior, en cambio, se produce cuando el
Sol se encuentra entre los planetas interiores y la
Tierra. En este caso, los planetas alcanzan su máxima distancia respecto a la
Tierra.
Una
conjunción gramatical, por su parte, es una
palabra invariable que encabeza una oración subordinada o que une
secuencias o vocablos sintácticamente equivalentes. Una conjunción
enlaza palabras, sintagmas o proposiciones.
En concreto, tendríamos que determinar que existen dos grandes grupos
de conjunciones. Por un lado, están las coordinantes y por otro, las
subordinantes.
Entre los más importantes tipos de conjunciones dentro del ámbito gramatical se encuentran las siguientes:
• Adversativa, que es aquella que viene a dejar patente una
confrontación o diferencia entre las dos oraciones. Ejemplos son “sin
embargo”, “pero”, “no obstante”, “excepto”…
• Comparativa. Es la que, como su propio nombre indica, sirve para
comparar ambas frases. En su caso, tendríamos que subrayar a “como”.
• Condicional, que es la conjunción que deja clara una condición que
debe darse para que tenga lugar una consecuencia. Un ejemplo de este
tipo es “si”.
• Copulativa, que podemos decir que viene a “sumar” las dos oraciones.
En este caso, los tipos de conjunciones son cuatro: “y”, “e”, “ni” y
“que”.
• Disyuntiva, que es la que viene a plasmar la contraposición de dos
frases o bien la alternancia o la exclusión de una de ellas. Son dos:
“o” y “u”.
“Al”,
“por”,
“para”,
“así que”,
“pese a que” y
“sino” son ejemplos de conjunciones:
“Al caer el sol, los vampiros salen de sus cuevas”,
“No vas a entrenar con nosotros por llegar tarde”,
“Estamos aquí para ayudar”,
“La decisión está tomada así que no insistas”,
“Pese a que te equivocaste, vas a tener otra oportunidad”,
“No fue Ricardo quien golpeó a Juan, sino Pedro”.
A todo ello tendríamos que añadir que en las matemáticas también se
emplea el término que nos ocupa. En su caso, existe lo que se conoce
como “conjunción lógica”, que viene a dejar patente que un operador
resulta verdadero si los dos operadores también lo son.
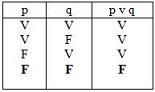Disyunción es la acción y efecto de desunir y separar. El concepto se utiliza en varios ámbitos, como la 
